本节书摘来自华章出版社《算法基础：打开算法之门》一书中的第3章，第3.6节，作者 ［美］托马斯 H 科尔曼（Thomas H Cormen），更多章节内容可以访问云栖社区“华章计算机”公众号查看

3.6 小结

在本章和上一章中，我们已经看到了关于查找的4个算法和关于排序的4个算法。我们将它们的特性总结在以下两个表中。因为第2章的3个查找算法仅仅是关于同一个题目的变形，我们将BETTERLINEARSEARCH或SENTINELLINEARSEARCH作为线性查找的代表均可。

这两个表中没有显示平均情况下的运行时间，因为除了典型的快速排序外，其他算法的平均情况下的运行时间均与最坏情况下的运行时间一致。我们已经学习了，当数组元素按顺序随机产生时，快速排序平均情况下的运行时间仅仅是Θ（nlgn）。这些排序算法在实际中进行对比的结果如何呢？我用C++将这些算法编写为程序，并且采取每4字节为一整数的数组存储，分别在两个不同的机器上运行了程序：一个机器是我的MacBook Pro（在这个机器上，我写了这本书），处理器为24 GHz Intel Core 2 Duo，内存为4 GB，系统为Mac OS 1068；另一个机器是一个Dell笔记本电脑（我的网络服务器），处理器为32 GHz Intel Pentium 4，内存为1 GB，系统为Linux version 262214。我使用g++和optimization level-O3来编译代码。我在规模可达到50000的数组上运行算法，且每个数组初始时均为逆序。针对每个规模的数组，我对每个算法运行20次，并计算出平均运行时间。

通过初始时将每个数组设为逆序，我抽取了插入排序和快速排序在最坏情况下的近似运行时间。因此，我运行了两个版本的快速排序：“普通”快速排序，它总是将子数组A［p…r］的最后一个元素A［r］被划分得到的位置元素作为主元，而随机快速排序总是在划分之前，将A［p…r］中随机选择的元素和A［r］进行调换。（此时我没有运行取3个数的中位数作为主元的方法。）“普通”快速排序这一版本因为没有采取随机化也被称为确定的快速排序。它所执行的一系列操作在给定待排序的输入数组时均已经是预先确定的。

当满足n≥64时，在这两个计算机上，随机快速排序均是冠军。以下是针对不同输入规模，其他算法相对于随机快速排序算法的运行时间的比率。

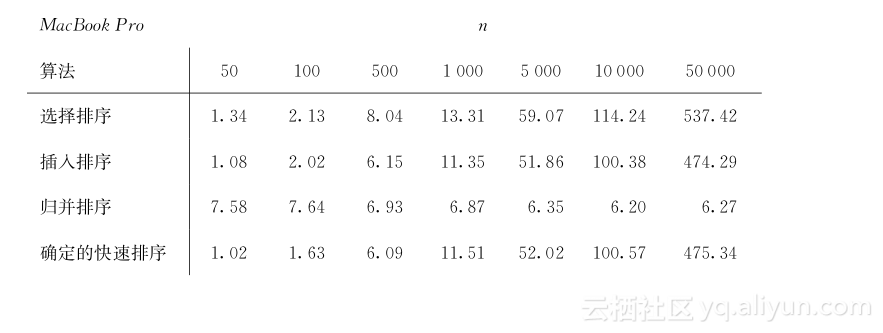
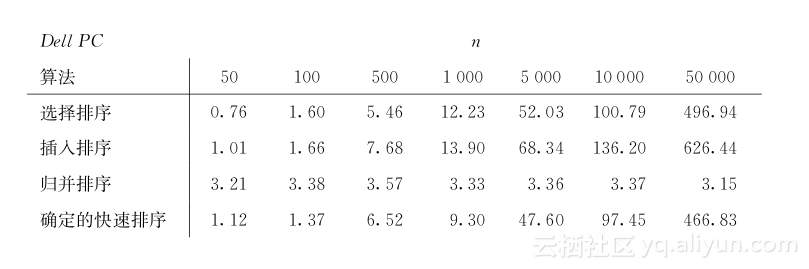
随机快速排序算法看起来很好，但是我们能够超越它。回忆一下，当所有数组中的元素均不需移动太远距离时，插入排序的运行效果很好。58一旦递归算法中子问题的规模降低到某个大小k时，每个元素的移动距离均不会超过k-1。因此当子问题规模变小时，我们并不需继续递归调用随机快速排序，反之可适当地更改排序子数组的算法而非运行整个数组的算法，例如在子数组上，我们运行插入排序会发生什么呢？确实，使用这样一种杂交方法，我们能够得到一个比随机快速排序更快速的排序算法。我发现在MacBook Pro上，子数组规模为22是最佳的交叉点，而在Dell PC上，子数组规模为17时是最佳的交叉点。以下是针对同一问题规模，在两个计算机上运行杂交算法相对于随机快速排序算法的运行时间的比率：

对于排序算法，是否有可能超越Θ（nlgn）的运行时间呢？这取决于具体情况。我们将在第4章看到如果只可以通过比较元素来确定数组中元素的位置，且执行其他操作均需以排序比较的结果为基础，那么答案是不能，我们不可能超越Θ（nlgn）的运行时间。但是如果知道关于这些元素的一些特性，我们就可以得到更短的运行时间。